Transient equilibrium
In nuclear physics, transient equilibrium is a situation in which equilibrium is reached by a parent-daughter radioactive isotope pair where the half-life of the daughter is shorter than the half-life of the parent. Contrary to Secular equilibrium, the half-life of the daughter is not negligible compare to parent's half-life. An example of this is the Molybdenum 99 generator producing Technetium 99 for nuclear medicine diagnostic procedures. Such a generator is sometimes called cow because the daughter product, in this case Technetium 99 is milked at regular intervals.[1] Transient equilibrium occurs after four half-lives, on average.
Contents |
Activity in transient equilibrium
The activity of the daughter is given by the Bateman equation:
![A_d = ([A_P(0)\frac{\lambda_d}{\lambda_d-\lambda_P} \times (e^{-\lambda_Pt}-e^{-\lambda_dt})] \times BR ) %2B A_d(0)e^{-\lambda_dt}](/2012-wikipedia_en_all_nopic_01_2012/I/a4b46f2887b227d3c3ab2b6433da6596.png) ,
,
where 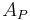 and
and 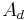 are the activity of the parent and daughter, respectively.
are the activity of the parent and daughter, respectively. 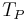 and
and 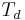 are the half-lives of the parent and daughter, respectively, and BR is the branching ratio.
are the half-lives of the parent and daughter, respectively, and BR is the branching ratio.
In transient equilibrium, the Bateman equation cannot be simplified by assuming the daughter's half-life is negligible compared to the parent's half-life. The ratio of daughter-to-parent activity is given by:
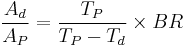 .
.
Time of maximum daughter activity
In transient equilibrium, the daughter activity increases and eventually reaches a maximum value that can exceed the parent activity. The time of maximum activity is given by:
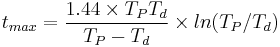 ,
,
where 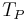 and
and 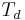 are the half-lives of the parent and daughter, respectively. In the case of
are the half-lives of the parent and daughter, respectively. In the case of 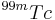 -
-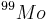 generator, the time of maximum activity (
generator, the time of maximum activity (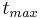 ) is approximately 24 hours which makes it convenient for medical use. [2]
) is approximately 24 hours which makes it convenient for medical use. [2]
See also
References
- ^ transient equilibrium
- ^ S.R. Cherry, J.A. Sorenson, M.E. Phelps (2003). Physics in Nuclear Medicine. A Saunders Title; 3 edition. ISBN 072168341X.